Problemas de ecuaciones cuadráticas

• Aquí van los pasos generales: Identifica los coeficientes de la ecuación de segundo grado o cuadrática. Esto es, debes escribir y tener bien claro quiénes son a, b y c. Te recomiendo escribirlos de este modo (que incluye dejar anotado al opuesto de b, es decir -b, a quien necesitarás más adelante para la fórmula de resolución).
  a=...
  b=... -b=...
  c=...
• Calcula el discriminante. Como recordarás, llamamos discriminante al valor que está debajo del radical de la fórmula de resolución. Hablamos de Δ=b2−4ac
• Analiza el resultado de ese discriminante. Ese resultado te dará la pista para saber si la ecuación tiene una, dos o ninguna solución en el campo de los números reales. Esto lo sabrás, según el discriminante sea mayor, igual o menor a cero.

Usa la fórmula cuadrática para obtener las mencionadas soluciones.

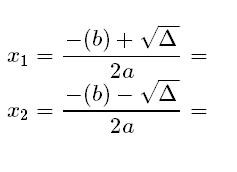
• Simplifica las soluciones si es posible y finaliza la resolución explicitando claramente la o las soluciones halladas, incluso si la ecuación no tuviera soluciones reales.

Ejemplo de resolución de una ecuación cuadrática

Se trata de aplicar los pasos señalados anteriormente, a un ejemplo concreto.

La ecuación que queremos resolver en este caso es la siguiente:

x2+2x-3= 0

Calcula el discriminante, vale decir: Δ=b2−4ac

En este caso, Δ= b2−4ac= (2)2−4(1)(−3)=16

• Analizar el resultado de ese discriminante. En este caso, el discriminante ha sido 16, esto es: discriminante mayor que cero. Cuando el discriminante es mayor que cero, inmediatamente podemos aseverar que esta ecuación tiene dos raíces o soluciones diferentes y pertenecientes al conjunto de los números reales.

Usar la fórmula cuadrática para obtener las mencionadas soluciones. Para este ejemplo, esto quedaría planteado de la siguiente forma:

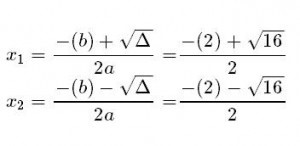
• Por último, hemos de realizar las operaciones correspondientes y simplificaciones en caso que corresponda con el objetivo de llegar a determinar cuánto valen las respectivas soluciones (recordarás que en el paso en que analizamos el discriminante, ya determinamos que serán dos, distintas y pertenecientes al conjunto de los números reales. El resultado de las mismas en este caso, es el siguiente.

x1= 1  ,  x3= -3

GLOSARIO

Coeficiente: es sinónimo de cifra, factor o proporción.